I have implemented RSA encryption and decryption using C++, along with support functions such as key generation. This implementation is purely academic and does not take into consideration many important real-world security issues. Several of the multiple precision integer algorithms were developed and implemented from the book Handbook of Applied Cryptography. I wrote some documentation for my implementation, which may be helpful if you are making your own implementation.
This implementation supports both single precision and multiple precision (a.k.a. big integer) mathematics. Several optimised functions are implemented including Barrett Modular Reduction.
This code is suitable for key size up to 1024 bits on modern computer.
Multiplication by Repeated Doubling
The multiple precision implementation contains a unique division algorithm by repeated doubling.
// This implementation was slower than another method I used, so I called this one 'slow', despite being fairly fast.
bool Integer::setFractionSlow(const Integer & numerator, const Integer & denominator, Integer & remainder) {
// Check to ensure there is a non-zero numerator for division.
if (numerator == 0) {
remainder = 0;
(*this) = 0;
return true; // no remainder
}
// Sanity checking...
if (denominator == 0) {
throw std::runtime_error("Division by 0!");
}
(*this) = 0; // Number of divisions possible e.g. the quotient.
Integer accumulator = 0; // Total value of doublings.
// This pair must typically be shifted together.
Integer count = 1;
Integer product = denominator;
// Main loop:
// The quotient is stored in this
// The invariant is that denominator * quotient < numerator at all times
// and count/product are always shifted together.
// Product starts out as the denominator, and is doubled or halved each time through the loop.
while (true) {
// We take the denominator, and add the accumulator.
Integer tmp = product;
tmp.add(accumulator);
// We check to see if we have reached the top or gone beyond it
// e.g. we have found denominator * (quotient + count) >= numerator
int s = tmp.compareWith(numerator);
// if denominator * (quotient + count)
if (s == 0) {
// We have found a division with no remainder
// e.g. denominator * (quotient + count) == numerator
this->add(count);
remainder = 0;
return true;
} else if (s == 1) {
// We have found a division with a remainder
// e.g. denominator * (quotient + count) > numerator
count.shiftRight(1);
product.shiftRight(1);
if (count == 0) {
// We have found a divisor with a remainder
remainder = numerator;
remainder.subtract(accumulator);
return false;
}
continue;
}
// denominator * (quotient + count) < numerator, so it is safe to increase the quotient by count.
this->add(count);
accumulator.add(product);
// We double count, and keep track of the product.
count.shiftLeft(1);
product.shiftLeft(1);
}
}The main benefit of this approach is that it only uses additions and shifts to perform division. This algorithm can probably be extended to support multi-core implementation and is very robust.
This diagram shows the process going on inside the algorithm when computing 30/5.
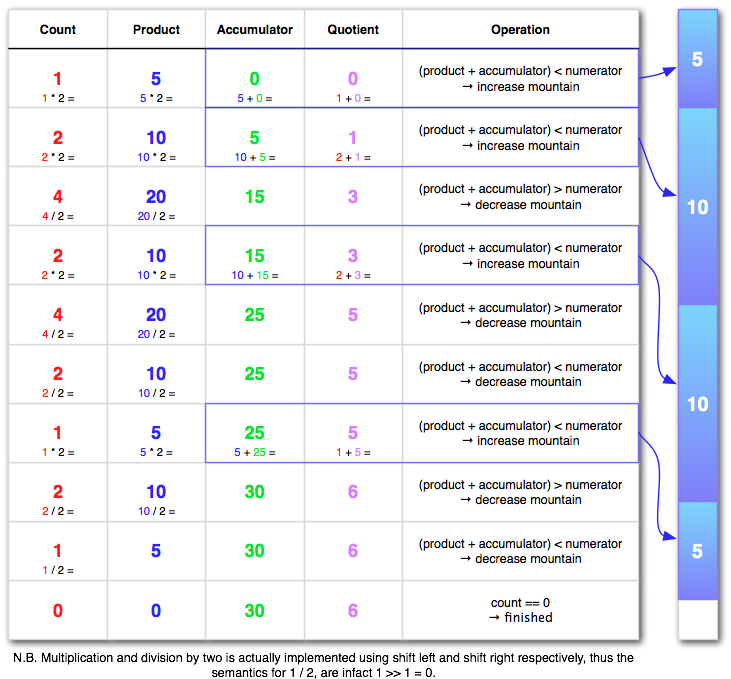
I suspect that the ramping up happens in logaritmic time, but on the way down we zig-zag many times, possibly as bad as linear time. I wonder if its possible to improve this? It might be possible to cache the results on the way back to avoid oscilations.
Usage
The source code is available as an Xcode project. This project may not be reproduced except for personal use.